Attracted by iris data
#JAはじめに
ここ数年「AI」という単語を耳にタコができるぐらい聞いて、結局なんのことか本質を掴めず、
このままだと「なんかデータをいっぱい突っ込めばいい感じにやってくれる」という間違った認識に飲み込まれそうなので、
今回は「データを観る」という原点に立ち返り、irisデータを使ってデータ予測の一端に触れてみます。
データセット
今回扱う下記アヤメ(iris)データは、“versicolor”, “setosa”, “virginica” という 3 種類の品種のアヤメのがく片 (Sepal)、花弁 (Petal) の幅および長さを計測したデータです。
ただし元のデータの中から3つほどデータを選び、「Iris-unknown」として、格納しています。
https://github.com/RuBisCO28/Iris/blob/master/iris.csv
データセットの詳細
レコード数 150
カラム数 5
各カラムの構成
sepal length (cm) がく片の長さ
sepal width (cm) がく片の幅
petal length (cm) 花弁の長さ
petal width (cm) 花弁の幅
species 品種

お題
さて今回のお題は、このirisデータを使って下記3つのデータが3種類のどの品種に当たるかの分類をやってみます。
前述の通り、品種の部分はあとで答え合わせのために「Iris-unknown」として伏せておきます。
5.1,3.7,1.5,0.4,Iris-unknown
6.1,2.8,4.7,1.2,Iris-unknown
6.8,3.0,5.5,2.1,Iris-unknown
分類方法
さてどのように分類をしていきましょう。 色々とやり方はあると思いますが、今回はテーマである「データを観る」に沿ってまずは「Iris-unknown」を含めたデータを見ていきます。
各変数ごとの分布の違い
まずは、各変数ごとに分布の違いがないか見ていきます。
また各分布の中で「Iris-unknown」がどこに位置するかも合わせて見ていきます。
import pandas as pd
import seaborn as sns
import matplotlib.pyplot as plt
df = pd.read_csv('iris.csv', sep=',', header=None, names=('sepal_length','sepal_width','petal_length','petal_width','species'))
iris_species_arr = df['species'].unique()
# sepal_length
for index, item in enumerate(iris_species_arr):
data = df.query('species=="'+item+'"')['sepal_length']
sns.distplot(data,kde=False,rug=False,label=item)
plt.legend()
plt.show()
# sepal_width
for index, item in enumerate(iris_species_arr):
data = df.query('species=="'+item+'"')['sepal_width']
sns.distplot(data,kde=False,rug=False,label=item)
plt.legend()
plt.show()
# petal_length
for index, item in enumerate(iris_species_arr):
data = df.query('species=="'+item+'"')['petal_length']
sns.distplot(data,kde=False,rug=False,label=item)
plt.legend()
plt.show()
# petal_width
for index, item in enumerate(iris_species_arr):
data = df.query('species=="'+item+'"')['petal_width']
sns.distplot(data,kde=False,rug=False,label=item)
plt.legend()
plt.show()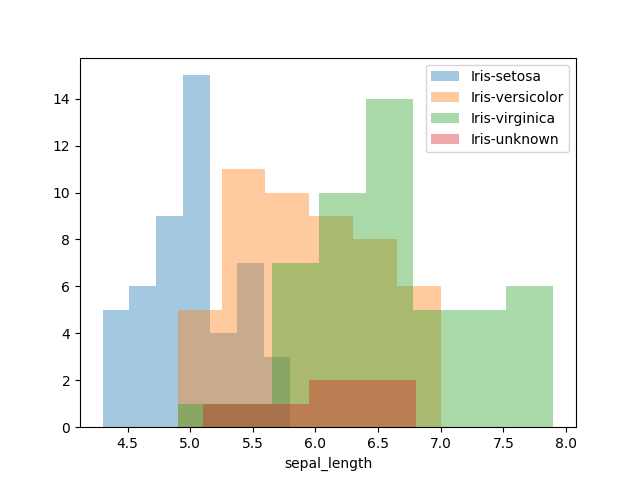
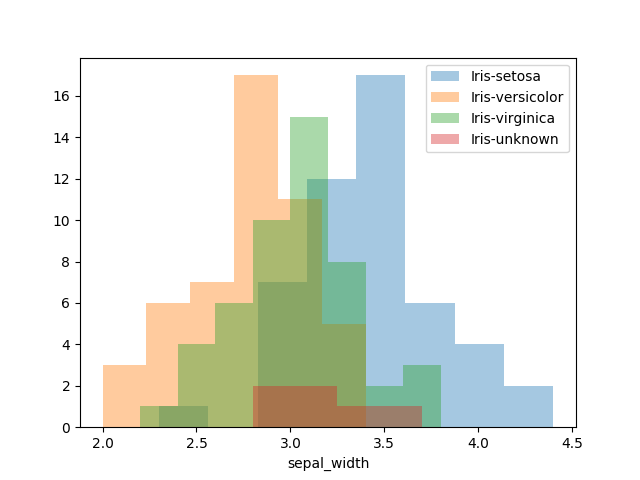
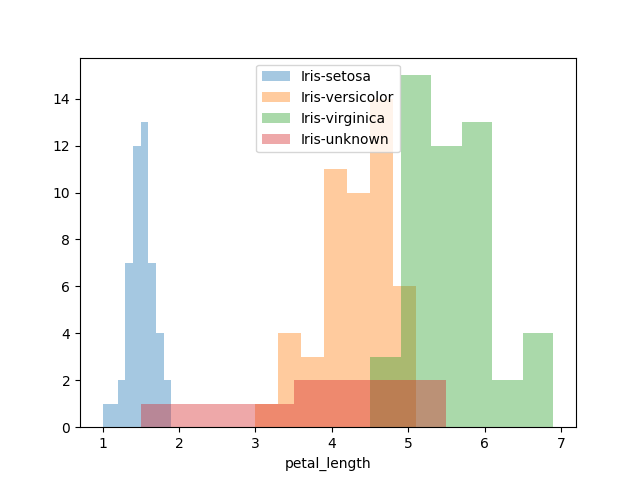
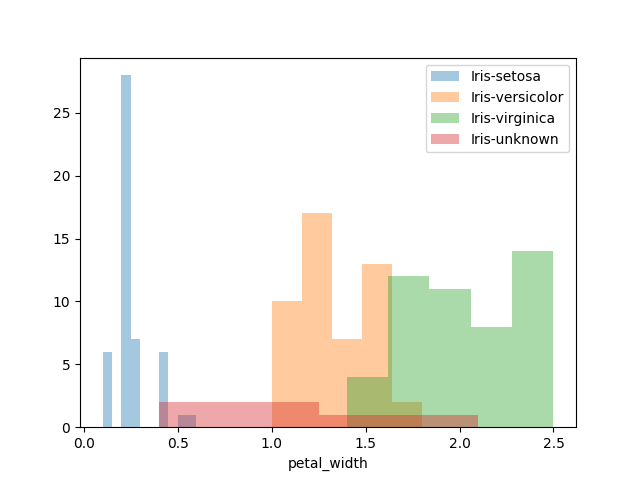
データの各変数の分布具合は見えました。
iris-setosaがほかの2種と分布が離れているように見えますが、予測するにはまだ不十分なため、もう少し詳しく見ていきます。
2変数の組み合わせによる分布の違い
さきほどは各変数ごとに見ていきましたが、今回は2変数の組み合わせで散布図を作成し、分布傾向を見ていきます。
g = sns.pairplot(df,hue = "species",diag_kind="kde")
plt.show()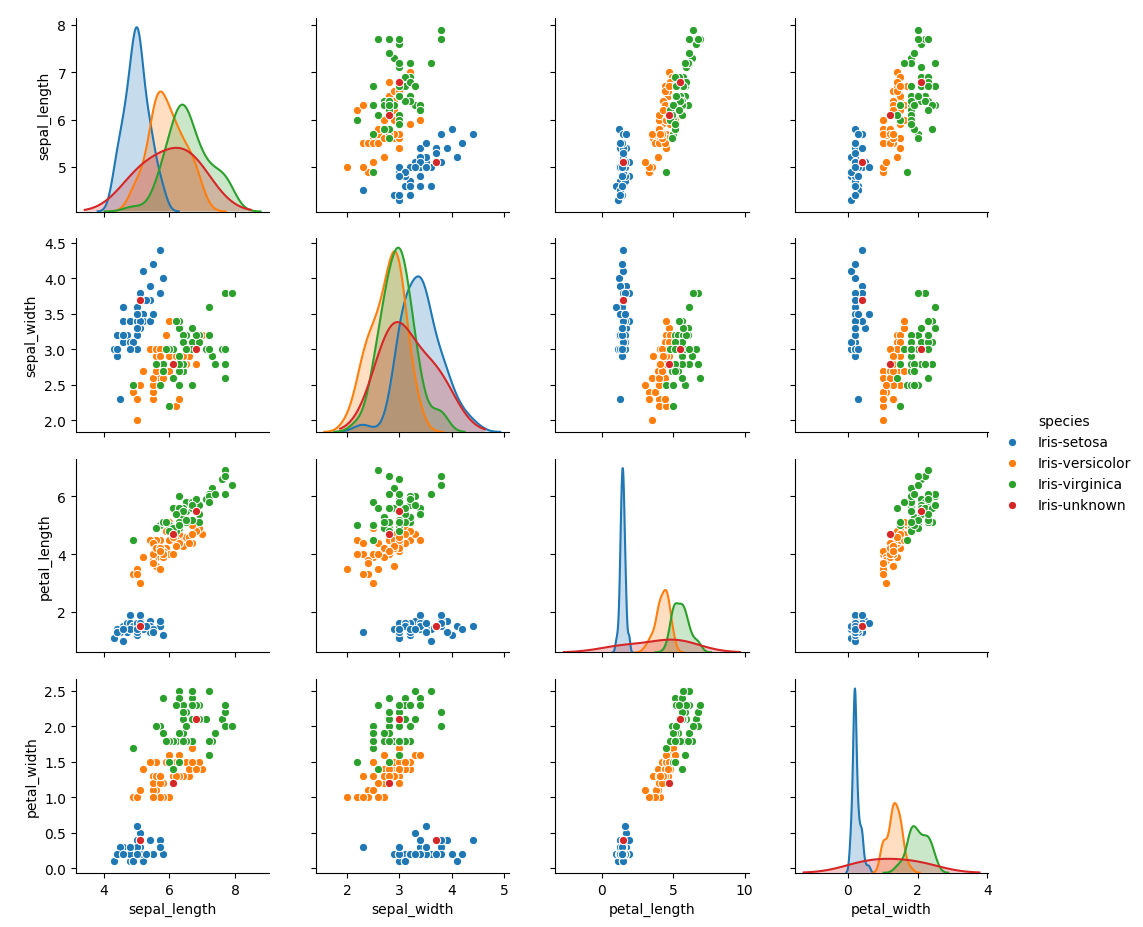
さていかがでしょうか?
赤丸がunknownですが、多くのpairplotでIris-setosaとかぶっているものがあります。
どうやら下記データは「Iris-setosa」のようです。
5.1,3.7,1.5,0.4,Iris-setosaで残りですが、petal_widthとsepal_widthの組み合わせ散布図を見るとそれぞれ分かれているので
下記データは、それぞれ「Iris-versicolor」,「Iris-virginica」と予測ができます。
6.1,2.8,4.7,1.2,Iris-versicolor
6.8,3.0,5.5,2.1,Iris-virginica
正解
正解は下記になります。 今回新しいデータではなく元のデータから選んだので、無作為に選んだとはいいがたいですが、分布図からある程度予測ができることが分かりました。
5.1,3.7,1.5,0.4,Iris-setosa
6.1,2.8,4.7,1.2,Iris-versicolor
6.8,3.0,5.5,2.1,Iris-virginica
最後に一言
今回機械学習には触れていませんが、データを可視化するだけでもある程度目星をつけることができました。
もちろん元のデータが良いというのもありますが、色々な角度からデータを見ることで新たな発見だったり、モデルを作りにしても 精度向上につながったりということがあるのでとても重要な作業です。